pe
The pe Rigid Body Physics Engine
Quick Facts
- Framework for massively parallel rigid body simulations
- Start of the project: 2006
- Developers:
- Former Developers:
- Klaus Iglberger
- Tobias Preclik
- Kristina Pickl
- Programming language: C++
Contents of the Research Project
The content of this research is the development of the pe physics engine. pe is an advanced C++ framework for the simulation of rigid, completely undeformable bodies with arbitrary shape. pe offers both collision solvers for physically accurate simulations as well as fast solvers suitable for computer games. The major focus of pe are large-scale and massively parallel rigid body simulations with up to several billion interacting rigid bodies. The currently largest simulations feature 10 billion bodies, 10 billion contacts on hundreds of thousands of processor cores of todays largest supercomputers.

The examples in Figure 2 through 9 show simulations of granular media with spherical and non-spherical and up to 720000 Particles. For these simulations up to 256 processes were used. Note that in comparison to the maximum possible number of processor cores these are comparatively small simulations. This is due to the fact that the size and number of the particles was chosen such that individual particles can still be distinguished in the visualization and the typical granular flow behavior can be seen. Further example pictures and videos of pe rigid body simulations can be found in our showroom.


The main problem for the simulation of frictional rigid body dynamics is the treatment of a linear complementarity problem of the following kind:
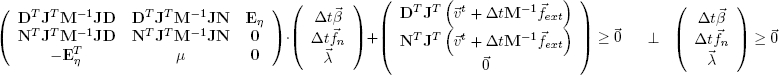
In order to solve this problem, pe offers several solvers, for instance the classical Lemke pivot algorithm, the projected Gauss-Seidel (PGS) algorithm, the conjugate projected gradient (CPG) algorithm, a damped Newton solver, and an algebraic multigrid (AMG) solver.

Features
- Software infrastructure for various rigid body simulation algorithms (DEM, RBD, …)
- Support for physically accurate rigid (multi-)body simulations
- Support for rigid body simulations in virtual reality environments
- Support for many parallelization concepts
- Shared memory parallelization (Threads, OpenMP, …)
- Distributed memory parallelization (MPI) pdf
- Exceptional C++ implementation satisfying the highest demands on software quality

Simulation Example

1 #include <pe/core.h> 2 #include <pe/util.h> 3 using namespace pe; 4 5 // The angle() function will be used to rotate the boxes by a small angle around the 6 // z-axis to make the appearance of the simulation more natural. The real return type 7 // is the preferred floating point data type of pe. Depending on the desired accuracy, 8 // real can be a single-precision or double-precision floating point type (whereas the 9 // default is double-precision). The random angles are generated by using one of the 10 // two templated rand() functions of the utiltiy module. The function arguments set 11 // the range of the generated random value. 12 real angle() 13 { 14 return rand<real>( -PI/20, PI/20 ); 15 } 16 17 int main() 18 { 19 const unsigned int timesteps( 1000 ); // Total number of time steps 20 const unsigned int height ( 14 ); // Height of the box stack 21 22 unsigned int id( 0 ); // User-specific ID counter 23 24 // One of the first actions in every pe simulation is the configuration of the 25 // simulation world. For instance, in this particular simulation, the gravity is 26 // set to -9.81 in -z-direction. 27 // Note that it is not necessary to explicitly destroy the world or the generated 28 // rigid bodies after the simulation has finished. The world will be automatically 29 // destroyed along with all contained rigid bodies. pe makes sure every object is 30 // destroyed if it is not needed any more. 31 WorldID world = theWorld(); 32 world->setGravity( 0.0, 0.0, -9.81 ); 33 34 // The first rigid body in the simulation world is the ground plane. The create 35 // function is responsible to automatically add the new plane to the world. The 36 // first argument sets the user-specific ID of the plane. The next four arguments 37 // set the normal or the plane and the displacement from the origin of the global 38 // world frame. With the last argument the material of the plane is specified. 39 createPlane( ++id, 0.0, 0.0, 1.0, 0.0, granite ); 40 41 // Setup of the wooden box stack 42 for( unsigned int i=height; i>0; --i ) { 43 for( unsigned int j=0; j<i; ++j ) 44 { 45 const Vec3 pos( -2.5*(i-1)+j*5.0, 0.0, 2.0+(height-i)*4.0 ); 46 47 // The next line creates a new box within the simulation world at the 48 // calculated position and with the box side lengths (4,4,4). The last 49 // parameter specifies the material of the box (oak wood). The function 50 // returns a handle to the newly created box. 51 BoxID box = createBox( ++id, pos, 4.0, 4.0, 4.0, oak ); 52 53 // The box is slightly rotated around the z-axis to improve the appearance 54 // of the simulation. This rotate() function takes three Euler angles in 55 // radian measure, one for each axis. 56 box->rotate( 0.0, 0.0, angle() ); 57 } 58 } 59 60 // This is the initialization of the metal sphere. The first argument of the 61 // createSphere() function is the user-specific ID, the next three values specify 62 // the global position of the center of the sphere. After this, the radius of the 63 // sphere is set to 1.5 and the material to iron. 64 SphereID sphere = createSphere( ++id, 0.0, -25.0, 8.0, 1.5, iron ); 65 66 // For making the sphere fly towards the box stack, the linear velocity of the 67 // sphere is initialized by 5.5 in y-direction and 0.1 in z-direction. 68 sphere->setLinearVel( 0.0, 5.5, 0.1 ); 69 70 // After the simulation setup, the simulation can be run. The run() function 71 // performs the specified number of time steps in the simulation world using 72 // a time step of 0.05 time units. The simulation will handle all rigid bodies 73 // according to the acting forces, their velocities, and will treat all collisions 74 // during this time span. 75 world->run( timesteps, 0.05 ); 76 }
Implementation Highlight: Smart Expression Templates
The pe has one of the stronges and most efficient C++ math libraries that are currently available. The special implementation based on Smart Expression Templates enables an architecture specific optimization of dense as well as sparse vector and matrix operations even for complex mathematical expressions. The following example gives a slight impression of the capabilities of the pe math library.
1 #include <pe/math.h> 2 using namespace pe; 3 4 int main() 5 { 6 // ... 7 8 // Creating four dense matrices of double precision 9 MatrixMxN<double> A( 600, 400 ), B( 600, 400 ), C( 400, 600 ), D( 400, 600 ); 10 MatrixMxN<double> E; 11 12 // Initializing the matrices 13 // ... 14 15 // Calculating the result of a complex dense matrix expression 16 // This calculation is automatically optimized at compile time based on the underlying 17 // architecture and runs with BLAS performance. 18 E = ( A + B ) * ( C - D ); 19 20 // ... 21 22 // Creating a dense matrix of 3x3 double precision matrices, a dense vector of 23 // 3D single precision vectors, and a sparse vector of sparse integer vectors 24 MatrixMxN< Matrix3x3<double> > M( 1000, 800 ); 25 VectorN< Vector3<float> > x( 800 ); 26 SparseVectorN< SparseVector<int> > y( 800 ); 27 28 // Initializating the matrix and the vectors 29 // ... 30 31 // Calculating the result of the complex mathematical expression 32 // The result is stored in a dense vector of 3D double precision vectors. 33 VectorN< Vector3<double> > v = M * x + y; 34 35 // ... 36 }


Downloads
The pe engine is subject to the GNU General Public License version 3 and comes with absolutely no warranty.
Please report back any problems encountered with the release candidate.
Publications
- Pickl, Kristina; Götz, Jan; Iglberger, Klaus; Pande, Jayant; Mecke, Klaus; Smith, Ana-Suncana; Rüde, Ulrich: All good things come in threes – Three beads learn to swim with lattice Boltzmann and a rigid body solver (Download)
In: Journal of Computational Science, 3(5) S. 374-387, 2012 - Preclik, Tobias; Rüde, Ulrich: Numerical Experiments with the Painlevé Paradox: Rigid Body vs. Compliant Contact (Download)
In: Joint International Conference on Multibody System Dynamics, May 29 – Jun 1, 2012, Stuttgart, Germany. S. I–X, 2012 - Götz, Jan; Donath, Stefan; Feichtinger, Christian; Iglberger, Klaus; Köstler, Harald; Rüde, Ulrich: waLBerla: Simulation of Complex Flows on Supercomputers (Download)
In: NIC Symposium 2012 – Proceedings. FZ Jülich, S. 349-356 (NIC Series), 2012 - Popa, Constantin; Preclik, Tobias; Köstler, Harald; Rüde, Ulrich: On Kaczmarz’s projection iteration as a direct solver for linear least squares problems (Download)
In: Linear Algebra and its Applications, 436(2) S. 389-404, 2012 - Preclik, Tobias; Popa, Constantin; Rüde, Ulrich: Regularizing a Time-stepping Method for Rigid Multibody Dynamics (Download)
In: Multibody Dynamics 2011. S. 78-79, 2011 - Götz, Jan; Iglberger, Klaus; Stürmer, Markus; Rüde, Ulrich: Direct Numerical Simulation of Particulate Flows on 294912 Processor Cores (Download)
In: IEEE computer society (Veranst.): 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis (Supercomputing ’10, New Orleans, 13.11. — 19.11.2010): S. 1-11, ISBN 978-1-4244-7559-9, 2010 - Götz, Jan; Iglberger, Klaus; Feichtinger, Christian; Donath, Stefan; Rüde, Ulrich: Coupling multibody dynamics and computational fluid dynamics on 8192 processor cores.
In: Parallel Computing 36(2-3): S. 142-151, 2010 - Iglberger, Klaus; Rüde, Ulrich: Large-scale Rigid Body Simulations
In: Multibody System Dynamics, 25(1): S. 81-95, 2010 - Iglberger, Klaus; Rüde, Ulrich: Massively Parallel Granular Flow Simulations with Non-Spherical Particles
In: Computer Science – Research and Development, 25(1-2): S. 105-113, 2010 - Preclik, Tobias; Iglberger, Klaus; Rüde, Ulrich: Iterative Rigid Multibody Dynamics (Download)
In: Arczewski, K.; Fracek, J.; Wojtyra, M. (Hrsg.): Multibody Dynamics 2009, ECCOMAS Thematic Conference (Multibody Dynamics 2009, Warsaw, 29.06.–02.07.2009). S. 1-17, ISBN 978-83-7207-813-1, 2009 - Iglberger, Klaus; Rüde, Ulrich: Massively Parallel Rigid Body Dynamics Simulations (Download)
In: Computer Science – Research and Development, 23(3): S. 159-167, 2009 - Götz, Jan; Feichtinger, Christian; Iglberger, Klaus; Donath, Stefan; Rüde, Ulrich: Large scale simulation of fluid structure interaction using Lattice Boltzmann methods and the “physics engine” (Download)
In: Mercer, G.N.; Roberts, A.j. (Hrsg.): Proceedings of the 14th Biennial Computational Techniques and Applications Conference, CTAC-2008 (14th Biennial Computational Techniques and Applications Conference, CTAC-2008, Canberra, AU, 13.07./ 16.07.2008) 2008, S. C166–C188 (ANZIAM Journal)
Technical Reports
- Preclik, Tobias; Rüde, Ulrich: Solution Existence and Non-Uniqueness of Coulomb Friction
Lehrstuhlbericht 04-2011 pdf - Popa, Constantin; Preclik, Tobias; Rüde, Ulrich: Iterative Regularized Solution of Symmetric and Positive Semi-Definite Linear Complementarity Problems
Lehrstuhlbericht 05-2011 pdf - Popa, Constantin; Preclik, Tobias: Iterative Solution of Weighted Least Squares Problems with Applications to Rigid Multibody Dynamics
Lehrstuhlbericht 10-10 pdf - Preclik, Tobias; Rüde, Ulrich; Popa, Constantin: Resolving Ill-posedness of Rigid Multibody Dynamics
Lehrstuhlbericht 10-11 pdf - Popa, Constantin; Preclik, Tobias; Köstler, Harald; Rüde, Ulrich: Some projection-based direct solvers for general linear systems of equations
Lehrstuhlbericht 10-6 pdf - Preclik, Tobias; Rüde, Ulrich: Elastic Collisions in Compementarity-based Time-stepping Methods
Lehrstuhlbericht 10-9 pdf - Iglberger, Klaus; Rüde, Ulrich: The Logging Functionality of the pe Physics Engine
Lehrstuhlbericht 10-1 pdf - Iglberger, Klaus; Rüde, Ulrich: Setup of Large-Scale Rigid Multibody Simulations with the pe Physics Engine
Lehrstuhlbericht 09-19 pdf - Iglberger, Klaus; Rüde, Ulrich: C++ Design Patterns: The Sandwich Pattern
Lehrstuhlbericht 09-18 pdf - Iglberger, Klaus; Rüde, Ulrich: The Math Library of the pe Physics Engine – Combining Smart Expression Templates and BLAS Efficiency
Lehrstuhlbericht 09-17 pdf - Iglberger, Klaus; Rüde, Ulrich: A C++ Vector Container for Pointers to Polymorphic Objects
Lehrstuhlbericht 09-11 pdf - Iglberger, Klaus; Rüde, Ulrich: C++ Compile Time Constraints
Lehrstuhlbericht 09-10 pdf - Iglberger, Klaus; Rüde, Ulrich: The pe Rigid Multi-Body Physics Engine
Lehrstuhlbericht 09-9 pdf - Iglberger, Klaus; Rüde, Ulrich: Massively Parallel Rigid Multi-Body Dynamics
Lehrstuhlbericht 09-8 pdf - Götz, Jan; Iglberger, Klaus; Feichtinger, Christian; Donath, Stefan; Deserno, Frank; Rüde, Ulrich: Comparing strategies for parallelizing large scale fluid structure interaction using lattice Boltzmann methods and a physics engine
Lehrstuhlbericht 09-7 pdf
